AES GCM and AES GCM-SIV mode

AES-GCM: Galois Counter Mode:

This is a mode of block cipher that uses universal hashing to provide authenticated encryption with associated data (AEAD), which is crucial to assure the data confidentiality and authenticity.

Elements of AES-GCM:

1. We will need a block cipher - any block cipher will work but in this senerio we will insist on AES.
2. Two function - Authenticated Encryption and Authenticated Decryption.
3. An authenticator function GHASH.

Authenticated Encrytion:

Input:

• Plaintext or message (P or msg).
• Additional authenticated data (AAD), denote aad.
• An initialization vector (IV).

Contrains:

• len(P) \(\leq 2^{39}-256\)
• len(aad) \(\leq 2^{64}-1\)
• 1 \(\leq\) len(IV) \(\leq 2^{64}-1\) but is recommended to len(IV) = 96 bit - 12 bytes.

Output:

• Ciphertext - CT. With len(CT) = len(msg)
• An authentication tag, or tag, for short, denoted T.

Authenticated Decryption:

Input:

• Ciphertext and tag

Output:

• Plaintext P.
• or a special error code, denote as FAIL.

Details:

Note: we will denote a 0 bit string length s is \(0^s\), and the concatenation between 2 bit strings is denote as ||.

GHASH:

In AES we has learn about finite field arithmetic in $GF(2^8)$. Now for the tag calcucation will be done in $GF(x^{128})$.

For AES GCM, mapping from bytes to field is the same will normal AES operation, which mean:

\[1 || 0^{126} || 1 = x^{127}+1\]

Addition operation will remains the same, but multiplication will use irreducible modulus: $x^{128}+ x^7 + x^2 + x + 1$. The function will be illustrated by diagram.

Authenticated Encryption:

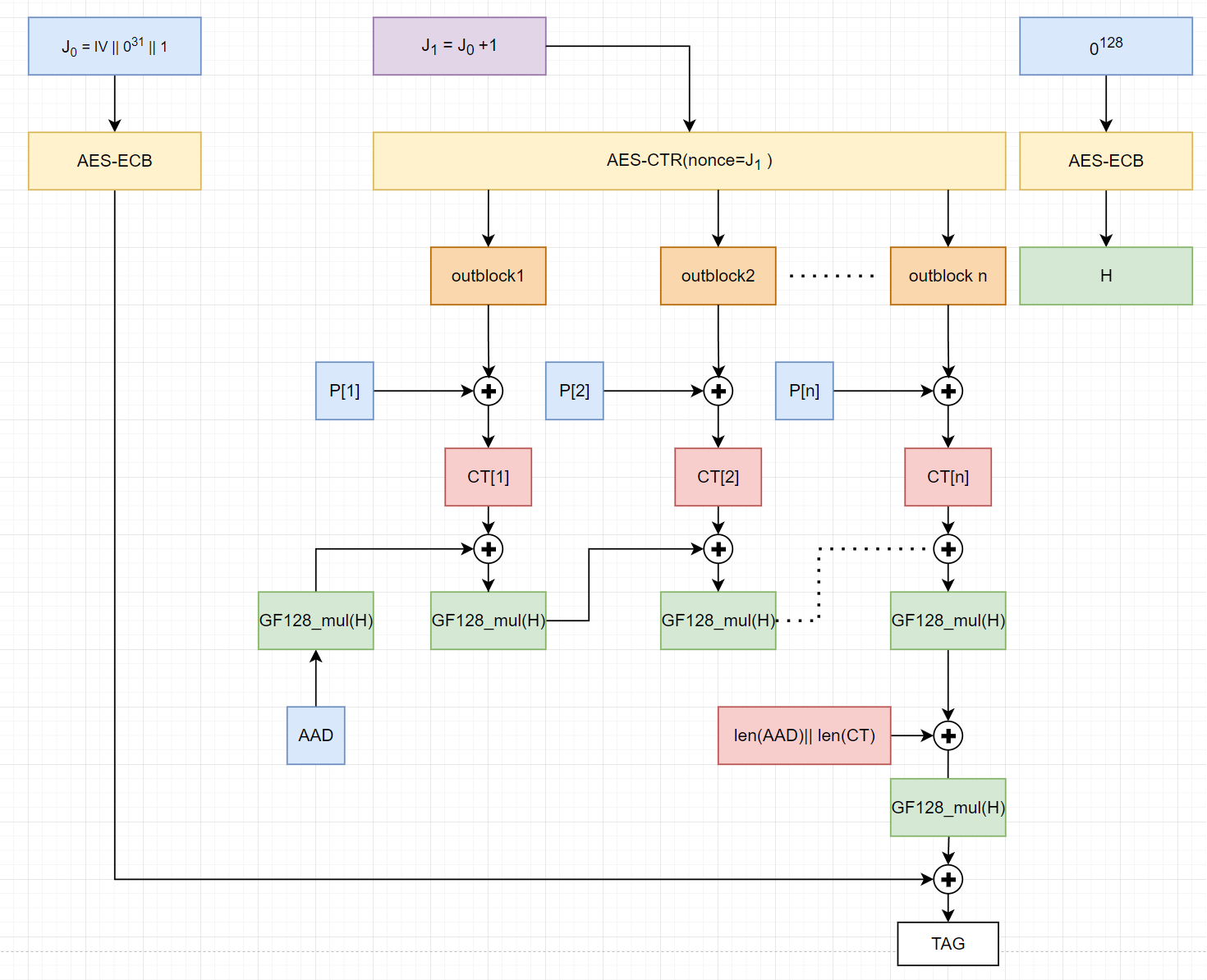
• Spectification:
  • $\text{Provided - Key(K), IV - will be fixed as 96 bits for easier calculatio.}$
  • $H = \text{AES_ECB_encrypt}(K,0^{128}).$
  • $J_0 = IV || 0^{31}|| 1. - 1 \; \text{to eliminate the case} \; H=J_0 \; \text{if} \; IV = 0^{96}$
  • $CT = \text{AES_CTR_encrypt}(KEY= K,Nonce = J_0 + 1,P) $
  • $\text{The Tag will be calculate by GHASH}$

Authenticated Decryption:

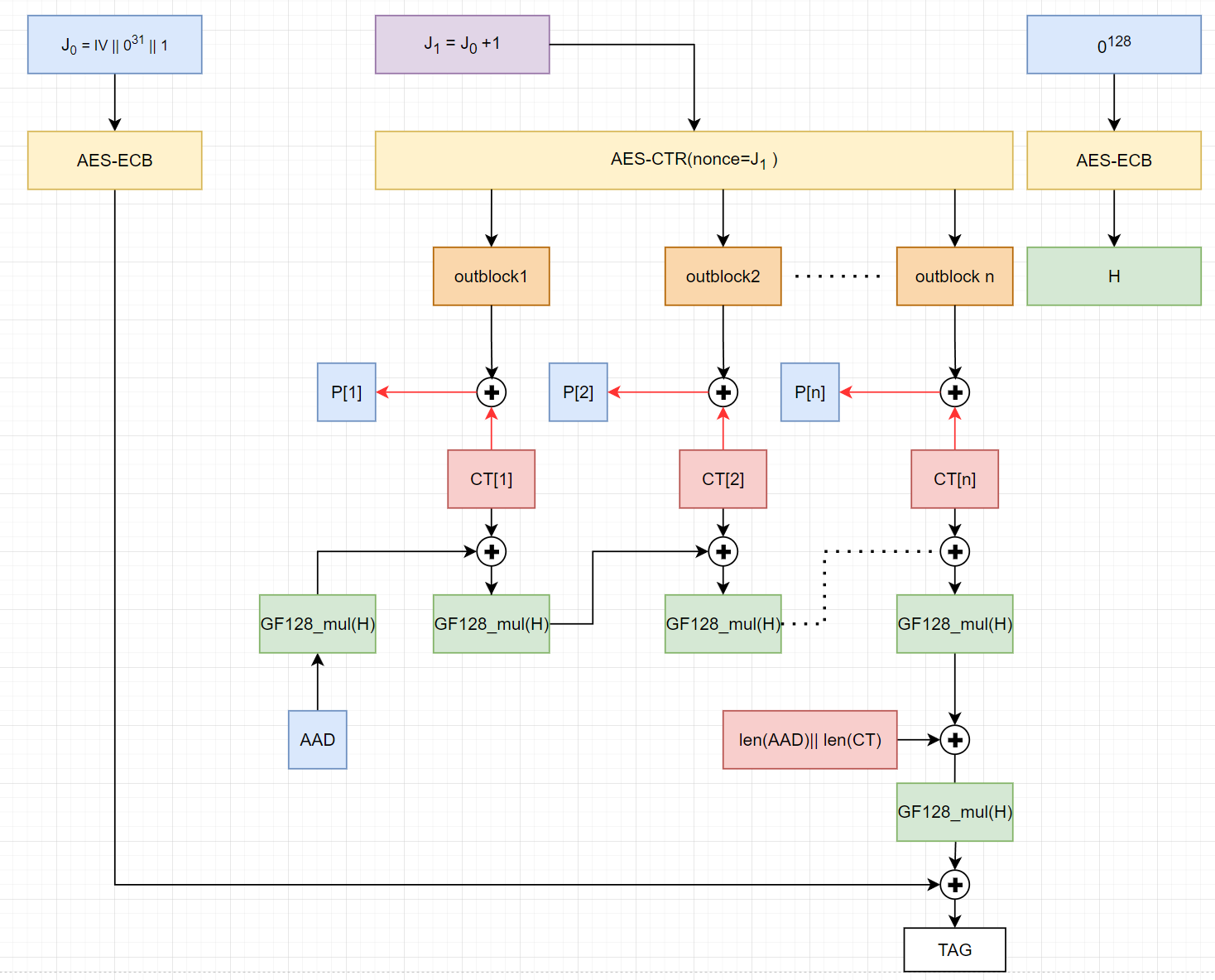
We can see that it mostly the same with encryption expect the red arrow. The Tag computed by the decryption process will be compared with the provided one to check integrity.

AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption

Many AEADS including AES-GCM suffer catastrophic failures of confidentiality and/or integrity when two distinct messages are encrypted with the same key and nonce. But nonce misuse-resistant AEADs like AES-GCM-SIV do not suffer from is problem.For this class of AEADs, encrypting two messages with the same nonce only discloses whether the messages were equal or not. This is the minimum amount of information that a deterministic algorithm can leak in this situation.

Elements of AES-GCM-SIV:

1. Block Cipher - AES.
2. Key derivation
3. Two function - Encryption and Decryption.
4. An authenticator function POLYVAL.

Details:

POLYVAL:

The field uses in POLYVAL is the same with GHASH - $GF(2^{128})$, but the reduction polynomial is $x^{128} + x^{127} + x^{126}+x^{121}+1$. We denote the field as $ \mathbb{F}$. Importantly, the mapping from bits to field element in this is different from mapping of GHASH or AES. It maps by convert bytes to bits but in reverse order - like little endian. E.g: “\x01” is 00000001 but in POLYVAL mapping will be 10000000.

Let “$\bullet$” for the operation in this field, for every $A_1$, $A_2$ $\in \mathbb{F}$.

\[A_1 \bullet A_2 = A_1 \oplus A_2 \oplus x^{-128}\]

So we have the POLYVAL$(H,X_1,X_2,..,X_n)$ = $\Sigma_{i=1}^{n}(X_i \bullet H_{n-i})$

Expanding it we have:

\[\Sigma_{i=1}^{n}(X_i \bullet H_{n-i}) = \Sigma_{i=1}^{n}(X_i \oplus H^{n-i+1} \oplus x^{-128\cdot(n-i+1)})\]

Let $w = H \cdot x^{-128}$, which make the implementing process easier 🥳.

\[\Sigma_{i=1}^{n}(X_i \oplus H^{n-i+1} \oplus x^{-128\cdot(n-i+1)}) = \Sigma_{i=1}^{n}(X_i \oplus w^{n-i+1})\]

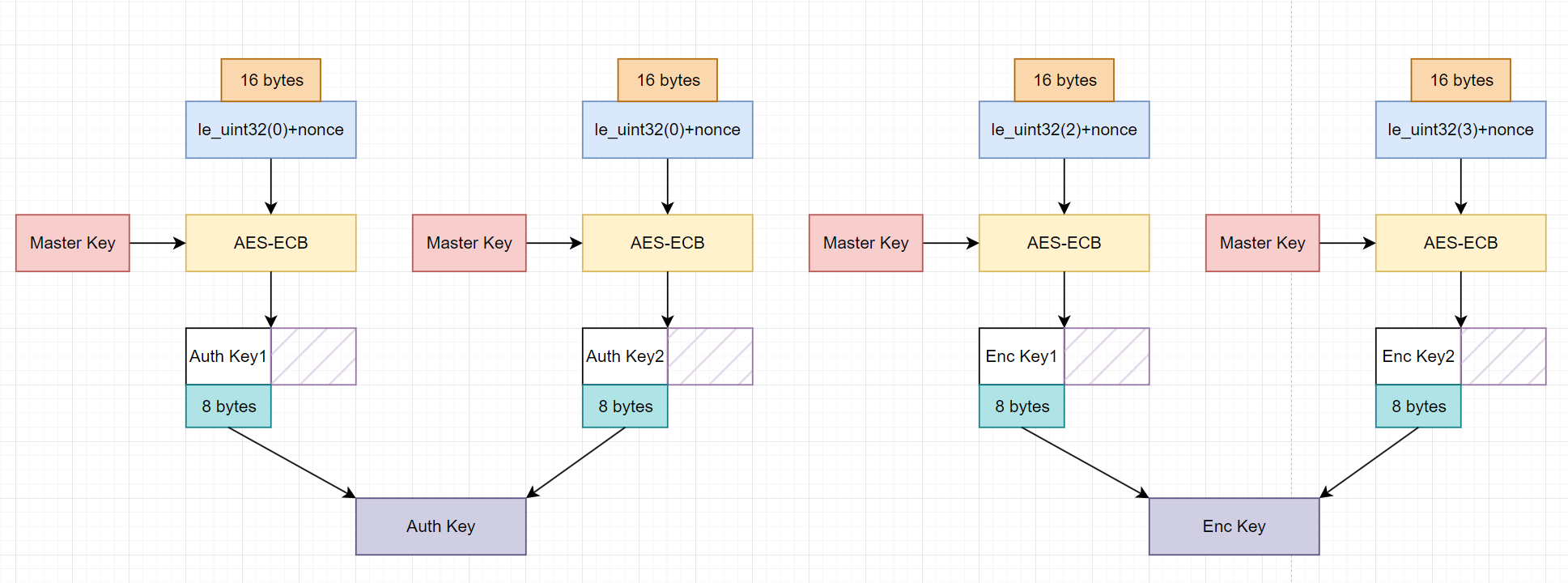
Key derivation:

We will have master key, and nonce, which wil use to generate message authentication key (msg_auth_key), and message encryption key (msg_enc_key) and to be used in next process

    func liitle_endian_uint32(n) {
        return bytes representation liite endian 32 bit 
        e.g little_endian_uint32(0) = \x00\x00\x00\x00
            little_endian_uint32(1) = \x01\x00\x00\x00
    }

    func derive_keys(master_key, nonce) {
      msg_auth_key =
          AES(key = master_key,
              block = little_endian_uint32(0) ++ nonce)[:8] ++
          AES(key = master_key,
              block = little_endian_uint32(1) ++ nonce)[:8]
      msg_enc_key =
          AES(key = master_key,
              block = little_endian_uint32(2) ++ nonce)[:8] ++
          AES(key = master_key,
              block = little_endian_uint32(3) ++ nonce)[:8]
 
      if bytelen(master_key) == 32 {
        msg_enc_key ++=
            AES(key = master_key,
                block = little_endian_uint32(4) ++ nonce)[:8] ++
            AES(key = master_key,
                block = little_endian_uint32(5) ++ nonce)[:8]
      }
      return msg_auth_key, msg_enc_key
    }

Encryption:

Input:

• Master Key - 16 bytes or 32 bytes. If master key is 16 bytes - AES-128 is used, alse AES-256 is used.
• AAD
• Nonce
• Plaintext

Output:

An authenticated ciphertext that will be 16 bytes longer than the plaintext.

   func right_pad_to_multiple_of_16_bytes(input) {
     while (bytelen(input) % 16 != 0) {
       input = input ++ "\x00"
     }
     return input
   }

   func AES_CTR(key, initial_counter_block, in) {
     block = initial_counter_block

     output = ""
     while bytelen(in) > 0 {
       keystream_block = AES(key = key, block = block)
       block[0:4] = little_endian_uint32(
           read_little_endian_uint32(block[0:4]) + 1)

       todo = min(bytelen(in), bytelen(keystream_block))
       for j = 0; j < todo; j++ {
         output = output ++ (keystream_block[j] ^ in[j])
       }
       in = in[todo:]
     }
     return output
   }

   func encrypt(master_key,
                nonce,
                plaintext,
                aad) {
     if bytelen(plaintext) > 2^36 {
       fail()
     }
     if bytelen(aad) > 2^36 {
       fail()
     }

     msg_enc_key, msg_auth_key = derive_keys(master_key, nonce)
    length_block =little_endian_uint64(bytelen(aad) * 8) ++ little_endian_uint64(bytelen(plaintext) * 8)
     padded_plaintext = right_pad_to_multiple_of_16_bytes(plaintext)
     padded_ad = right_pad_to_multiple_of_16_bytes(aad)
     S_s = POLYVAL(key = msg_auth_key, input = padded_ad ++ padded_plaintext ++ length_block)
     for i = 0; i < 12; i++ {
       S_s[i] ^= nonce[i]
     }
     S_s[15] &= 0x7f
     tag = AES(key = msg_enc_key, block = S_s)

     counter_block = tag
     counter_block[15] |= 0x80
     return AES_CTR(key = msg_enc_key, initial_counter_block = counter_block, in = plaintext) ++ tag
   }

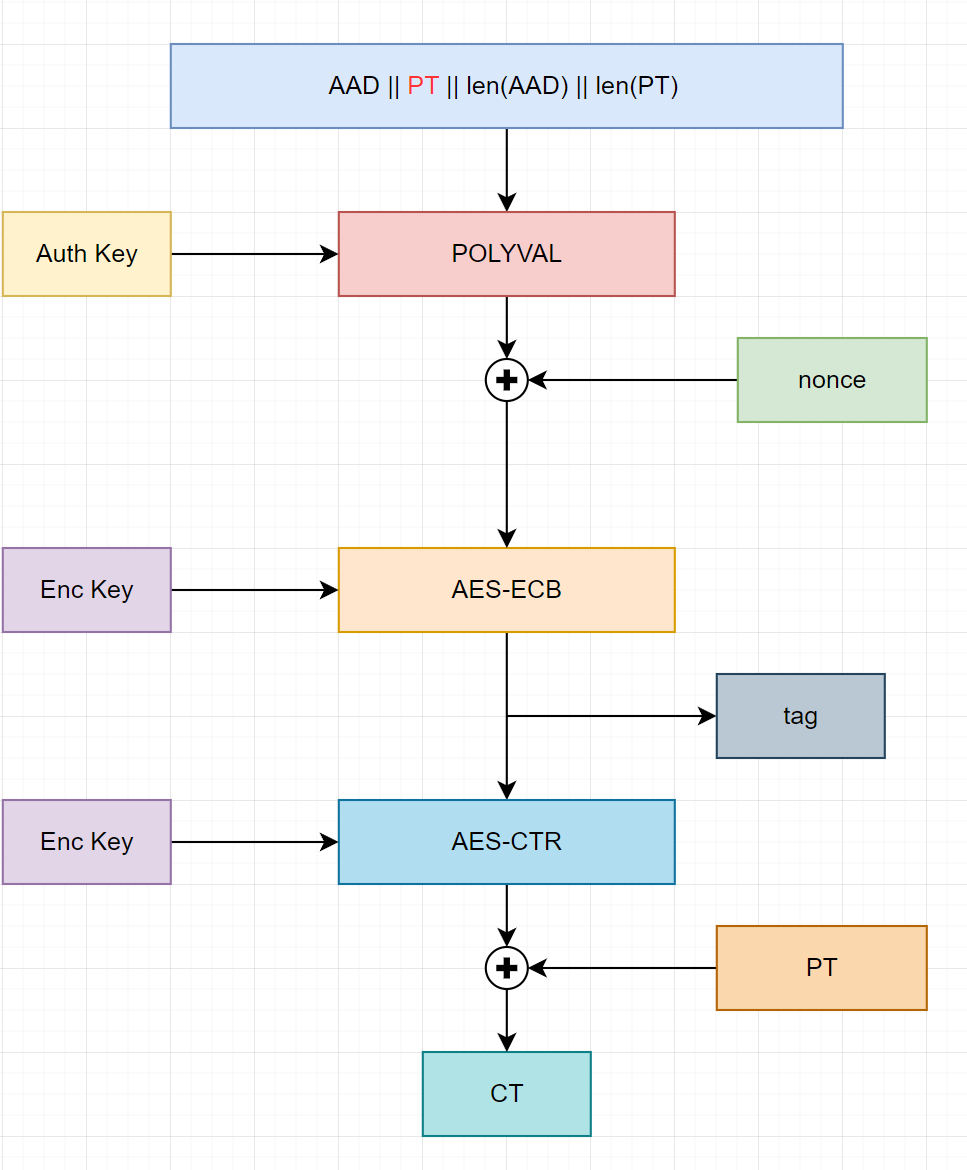
Note: We can easily distinguished GHASH and POLYVAL function:

\[GHASH = (aad \; \| \; CT \; \| \; len(aad) \; \| \; len(CT))\]

GHASH is calculated based on ciphertext, but POLYVAL is calculated by plaintext P.

\[POLYVAL = (aad \; \| \; P \; \| \; len(aad) \; \| \; len(P))\]

Decryption:

Input:

• Master Key - 16 bytes or 32 bytes. If master key is 16 bytes - AES-128 is used, alse AES-256 is used.
• AAD
• Nonce
• Ciphertext

Output:

• Plaintext or FAIL code.

   func decrypt(key_generating_key,
                nonce,
                ciphertext,
                aad) {
     if bytelen(ciphertext) < 16 || bytelen(ciphertext) > 2^36 + 16 {
       fail()
     }
     if bytelen(aad) > 2^36 {
       fail()
     }

     msg_enc_key, msg_auth_key =
         derive_keys(key_generating_key, nonce)

     tag = ciphertext[bytelen(ciphertext)-16:]

     counter_block = tag
     counter_block[15] |= 0x80
     plaintext = AES_CTR(key = msg_enc_key,
                         initial_counter_block = counter_block,
                         in = ciphertext[:bytelen(ciphertext)-16])

     length_block =
         little_endian_uint64(bytelen(aad) * 8) ++
         little_endian_uint64(bytelen(plaintext) * 8)
     padded_plaintext = right_pad_to_multiple_of_16_bytes(plaintext)
     padded_ad = right_pad_to_multiple_of_16_bytes(aad)
     S_s = POLYVAL(key = msg_auth_key,
                   input = padded_ad ++ padded_plaintext ++
                           length_block)
     for i = 0; i < 12; i++ {
       S_s[i] ^= nonce[i]
     }
     S_s[15] &= 0x7f
     expected_tag = AES(key = msg_enc_key, block = S_s)

     xor_sum = 0
     for i := 0; i < bytelen(expected_tag); i++ {
       xor_sum |= expected_tag[i] ^ tag[i]
     }

     if xor_sum != 0 {
       fail()
     }

     return plaintext
   }

References

1. NIST Special Publication 800-38D: Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC
   • Recommendations for GCM and GMAC block cipher modes.
2. NIST GCM Specification
   • Detailed specification of GCM by NIST.
3. RFC 8452: Online Authenticated-Encryption and Associated Data (AEAD) Algorithm for the AES-GCM and AES-CCM Modes of Operation
   • AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption
4. Cryptanalysis of Galois/Counter Mode of Operation (GCM)
   • Cryptanalysis of GCM and potential vulnerabilities.
5. Optimization of AES-GCM-SIV
   • Optimization techniques for AES-GCM-SIV.