Background
When doing picoCTF 2025, I encountered a challenge that requires to forge a TAG for a AEAD cipher ChaCha20-Poly1305 with a reused key and nonce. This post is a summary of the cipher and the attack.
ChaCha20-Poly1305
Like AES-GCM, ChaCha20-Poly1305 have two components: a encryption cipher and a tag generation part.
ChaCha20
ChaCha20 can be understood as a 20 rounds (80 quarter rounds) variant of ChaCha cipher - a stream cipher. It takes a 256-bit key, a 96-bit nonce, and a 32-bit counter to generate a keystream. The keystream is then xored with the plaintext to produce the ciphertext.
Internal
Quarter Round is the basic of Chacha cipher, which operate on 4 32-bit unsigned integers $a, b, c, d$ as follows, and denote as QUARTERROUND(a,b,c,d)
|
|
A state of ChaCha20 can be represented as 4x4 matrix of 32-bit unsigned integers.
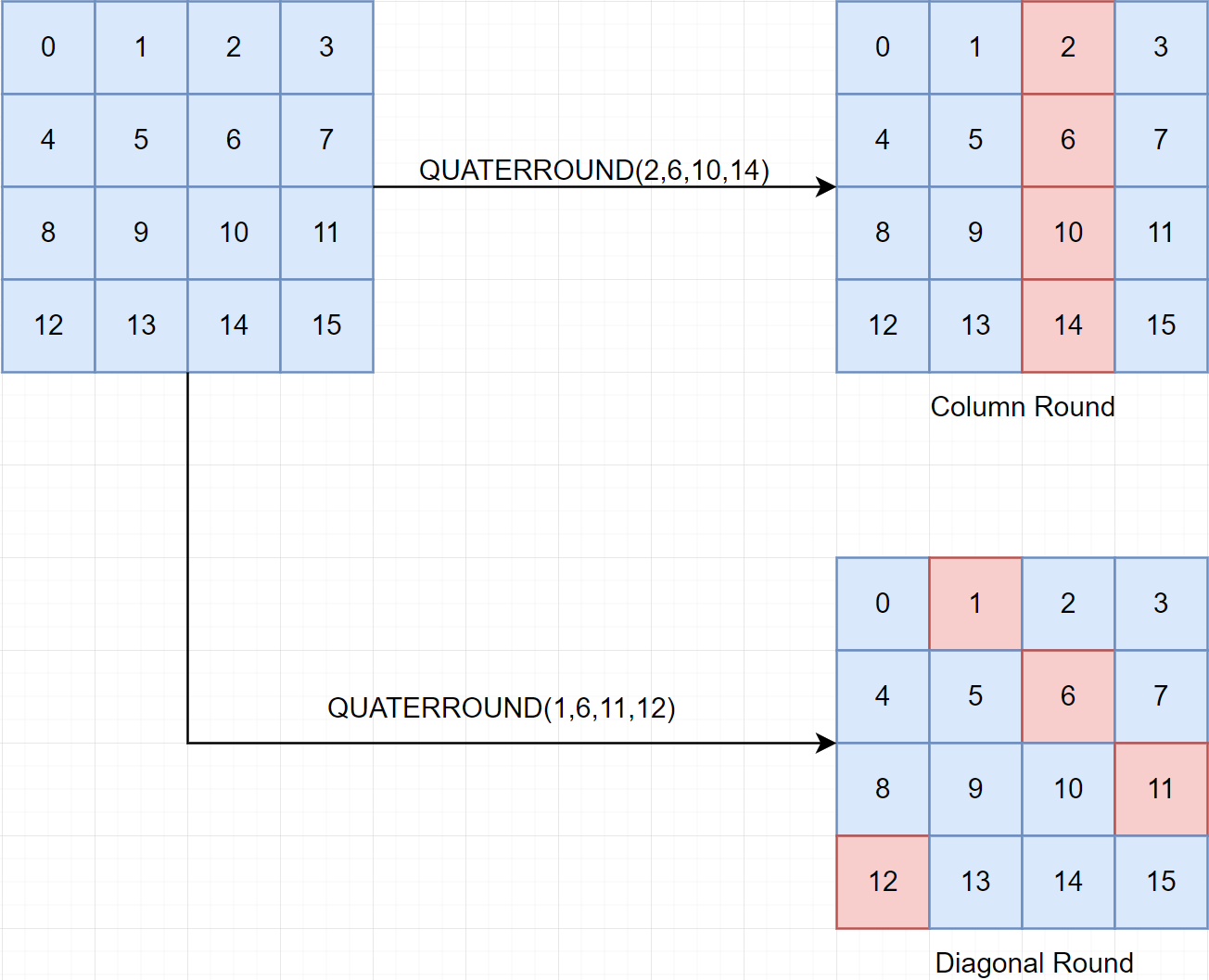
ChaCha20 runs 20 rounds with alternating between column rounds and diagonal rounds. Below present of 2 rounds. So it will run 10 iterations for the list of rounds below.
inner_block (state):
QUARTERROUND(state, 0, 4, 8,12)
QUARTERROUND(state, 1, 5, 9,13)
QUARTERROUND(state, 2, 6,10,14)
QUARTERROUND(state, 3, 7,11,15)
QUARTERROUND(state, 0, 5,10,15)
QUARTERROUND(state, 1, 6,11,12)
QUARTERROUND(state, 2, 7, 8,13)
QUARTERROUND(state, 3, 4, 9,14)
end
chacha20_block(key, counter, nonce):
state = constants | key | counter | nonce
working_state = state
for i=1 upto 10
inner_block(working_state)
end
state += working_state
return serialize(state)
end
Encryption
Because ChaCha20 is a stream cipher decryption is the same as encryption.
- Input:
- Key: 256-bit key.
- Nonce: 96-bit nonce.
- Counter $(J)$: 32-bit counter. In ChaCha20-Poly1305, the counter is set to 1 because block 0 is used to derive $(r,s)$ for Poly1305.
- Plaintext: arbitrary length plaintext.
- Output:
- Ciphertext: same length as plaintext.
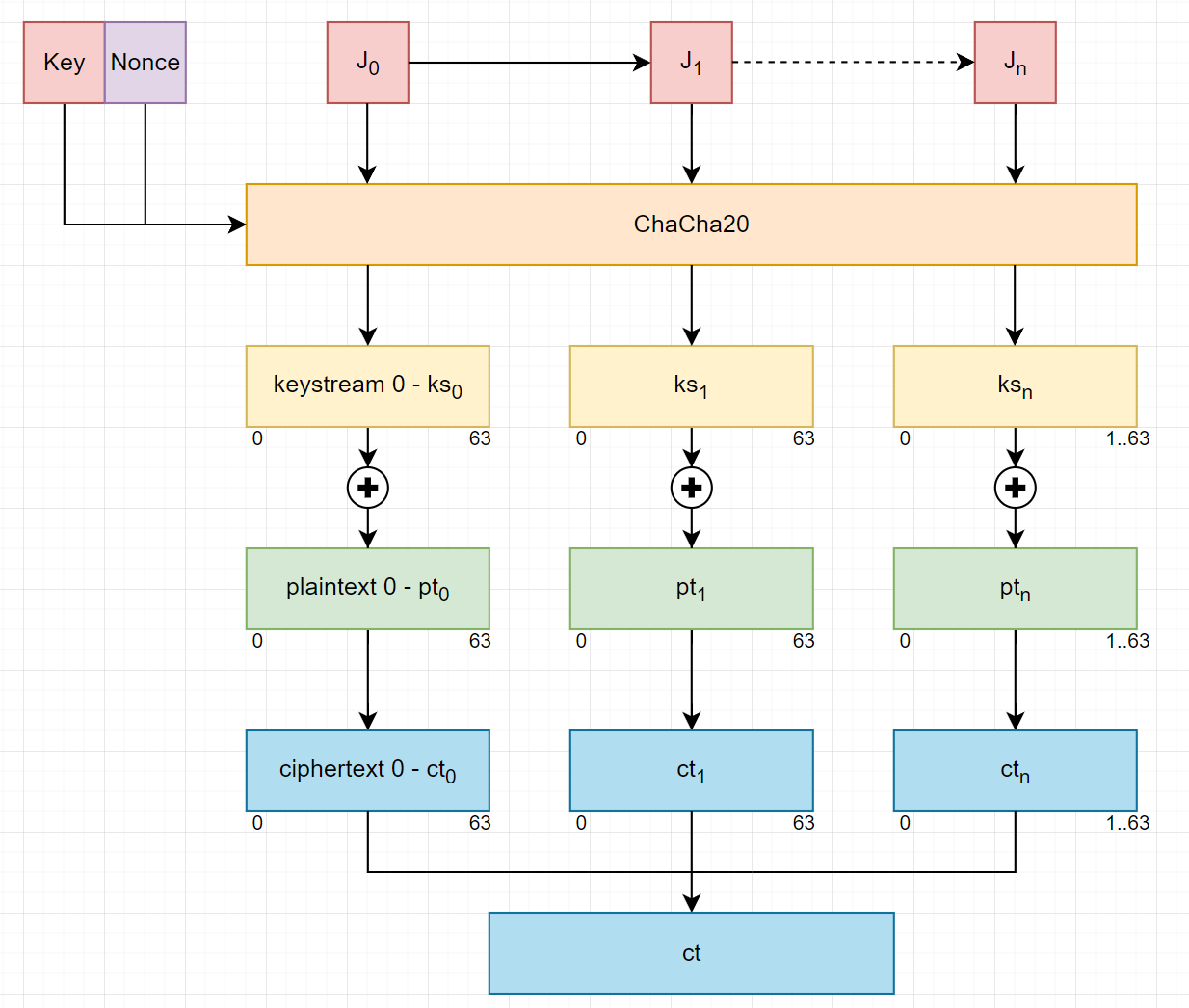
Note: all number in figure are for (0 .. 63) bytes = 512 bits.
- In pesudo code:
chacha20_encrypt(key, counter, nonce, plaintext):
for j = 0 upto floor(len(plaintext)/64)-1
key_stream = chacha20_block(key, counter+j, nonce)
block = plaintext[(j*64)..(j*64+63)]
encrypted_message += block ^ key_stream
end
if ((len(plaintext) % 64) != 0)
j = floor(len(plaintext)/64)
key_stream = chacha20_block(key, counter+j, nonce)
block = plaintext[(j*64)..len(plaintext)-1]
encrypted_message += (block^key_stream)[0..len(plaintext)%64]
end
return encrypted_message
end
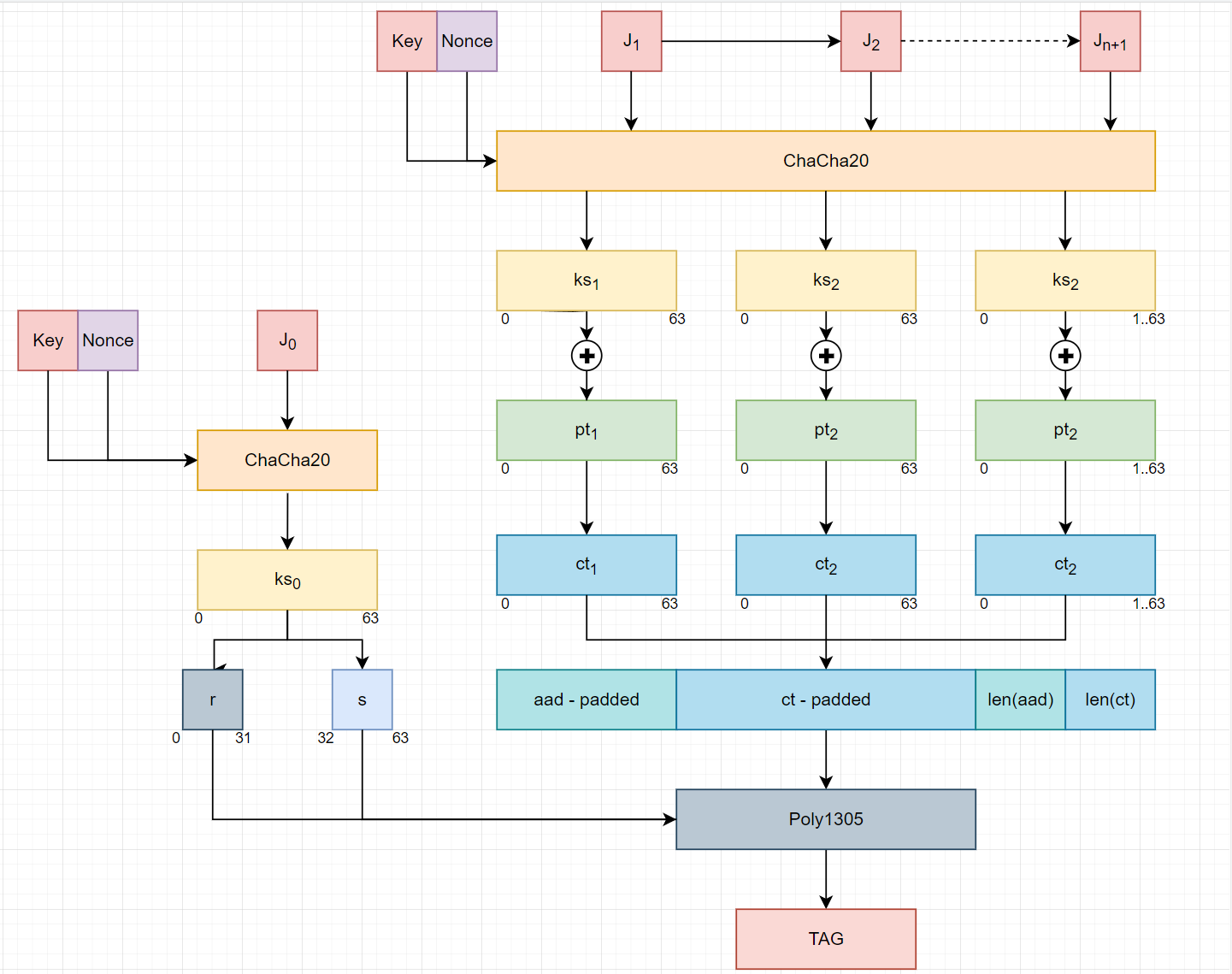
Poly1305
The original Poly1305 first appear in The Poly1305-AES message-authentication code. Briefly, It a MAC function requires 2 128-bits keys, and 1 128-bits nonce. AES used 1 key to encrypt nonce and compile with another key to have a pair $(r,s)$.
The pair $(r,s)$ must be unpredictable and follow the standard below. Here $r$ is treated as 16-octet little-endian number because of $C$ limitation.
-
r[3], r[7], r[11], and r[15] are required to have their top four bits clear (be smaller than 16)
-
r[4], r[8], and r[12] are required to have their bottom two bits clear (be divisible by 4)
And the Poly1305 function is as follow, because $msg$ when going into poly1305 have been padded to a multiple of 16 bytes so we don’t consider last block < 16 bytes.
|
|
So the Poly1305 function can be written as
$$\operatorname{Poly1305}(r, s, \mathrm{msg}) = \left(\left(\mathrm{block}_1 r^i + \mathrm{block}_2 r^{i-1} + \dots + \mathrm{block}_i r^1\right) \bmod (2^{130} - 5) + s\right) \bmod 2^{128}$$
$(r,s)$ pair generation for ChaCha20 is simple as follow.
|
|
ChaCha20-Poly1305 encryption/decryption.
Here is sanity check script.
Reuse Nonce attack:
In Oracle scheme, The key is often reused for multiple messages, but when Nonce is reused, we will have 2 $ct$ and $tag$ pairs from the same $(r,s)$ pairs
$$tag_1 = Poly1305(r, s, pad(ct_1)) = ((block_{1,1} r^i + block_{1,2} r^{i-1} + \dots + block_{1,i} r^1) \bmod (2^{130} - 5) + s) \bmod 2^{128}$$ $$tag_2 = Poly1305(r, s, pad(ct_2)) = ((block_{2,1} r^i + block_{2,2} r^{i-1} + \dots + block_{2,i} r^1) \bmod (2^{130} - 5) + s) \bmod 2^{128}$$ $$tag_1 - tag_2 = (r^i A_1 + r^{i-1} A_2 + \dots + r^1 A_i) \bmod (2^{130} - 5) \bmod 2^{128},\quad A_i = block_{1,i} - block_{2,i}$$ $$tag_1 - tag_2 = (r^i A_1 + r^{i-1} A_2 + \dots + r^1 A_i) + k 2^{128} \bmod (2^{130} - 5),\quad k \in \{-4, 4\}$$
From this we can recover $r$ easily and check if $r$ is correct by using clamp function and derive $s$ from $tag_1$ and $tag_2$ and check if equal. From $r,s$ we can forge a tag for any message using the keystream generated from ChaCha20.
Example.
Challenge ChaCha Slide in picoCTF 2025: We are given 2 pair (ct,tag) - known plaintext to get the keystream, and we need to forge a tag for a new message.
|
|
References
- ChaCha20 and Poly1305 for IETF Protocols
- Introduction to ChaCha20 and Poly1305.