Invisible Salamanders in AES GCM and AES GCM SIV
Introduction to the attack and proof of concept (POC).
Note: Information about AES - Advanced Encryption Standard and mode GCM, GCM-SIV can be read here.
Background:
When I come across the Invisible Salamander paper that described a way to bypass Facebook attachment franking scheme: a malicious user can send an objectionable image to a recipient but that recipient cannot report it as abuse. And a blog about this attack can work with AES GCM SIV.
For more details, it can be understand that we can construct a poison ciphertext and a tag that is valid under two different keys. One key will decrypt to the message we need, the other will decrypt to some trash value. The case in the paper, the attacker would make the attachment twice as long, with the first part decrypt to a abuse picture under key 1, and the second part a normal picture under key 2.
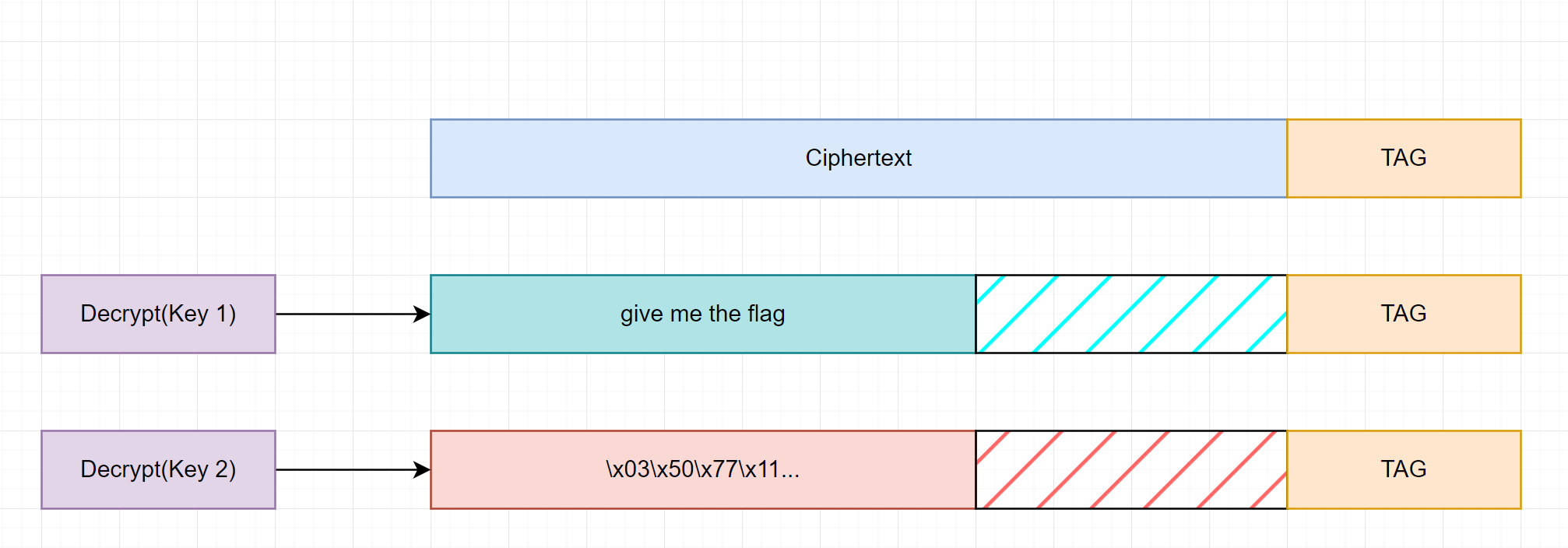Salamander example.
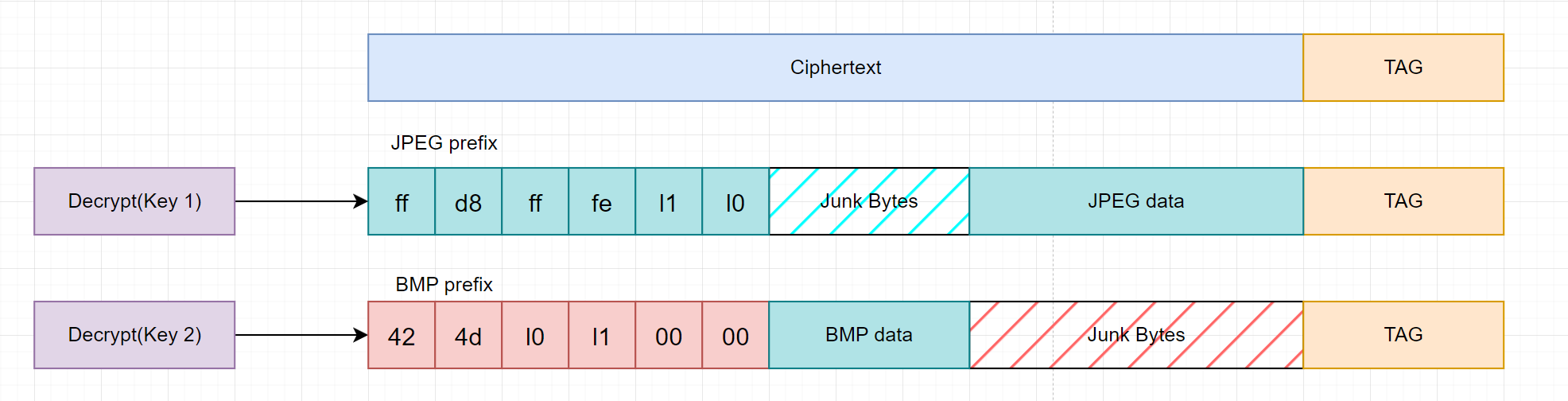Facebook attack.
Details:
Constructing Salamander on AES GCM:
About this mode of AES, see here. For easy when writing the equation, I will denote addition operation as “+” and multiplication as $\cdot$. In the blog (my blog or this), we can see that the GHASH function can be define as:
\[GHASH(H,C,T) = \Sigma_{i=0}^{n} (X_i \cdot H^{n-i+1}) + T = C_0 \cdot H^{n+1} + C_1 \cdot H^{n} + \dotsb + C_n \cdot H^{1} +T\]With H = AES_ECB_encryption(key,$0^{128}$), T = AES_ECB_encryption(key,IV $||$ $0^{31}$ $||$ 1), and C = AES_CTR(key,Plaintext,nonce = IV $||$ $0^{31}$ $||$ 2) is divided into blocks of 16 bytes $C_i$
To have a ciphertext that is valid under 2 different key. We need to fix the tag, that is $GHASH(H_1,C,T_1) = GHASH(H_2,C,T_2)$. And to achieve this we just add a sacrificial block append to the ciphertext (note: we can append and calculate it at any position, but for simplicity we will append it at the end of the ciphertext). So that the length of the poison ciphertext is one block more than normal ciphertext of that message.
\(\begin{align} \text{GHASH}(H_1, C, T_1) &= \text{GHASH}(H_2, C, T_2) \\ \sum_{i=0}^{n+1} (X_i \cdot H_{1}^{n+1-i}) + T_1 &= \sum_{i=0}^{n+1} (X_i \cdot H_{2}^{n+1-i}) + T_2 \\ C_j \cdot (H_1^{n+1-j} +H_2^{n+1-j})&= \sum_{i=0 \; \& \; i \neq j}^{n+1} X_i \cdot (H_1^{n+1-i} + H_2^{n+1-i}) + T_1 + T_2 \end{align}\) From this we can solve for $C_j$.
Variants:
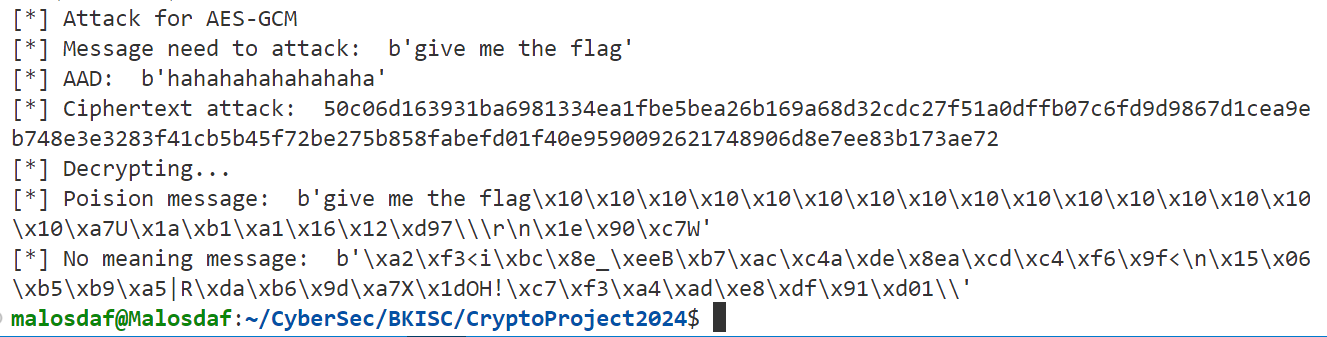
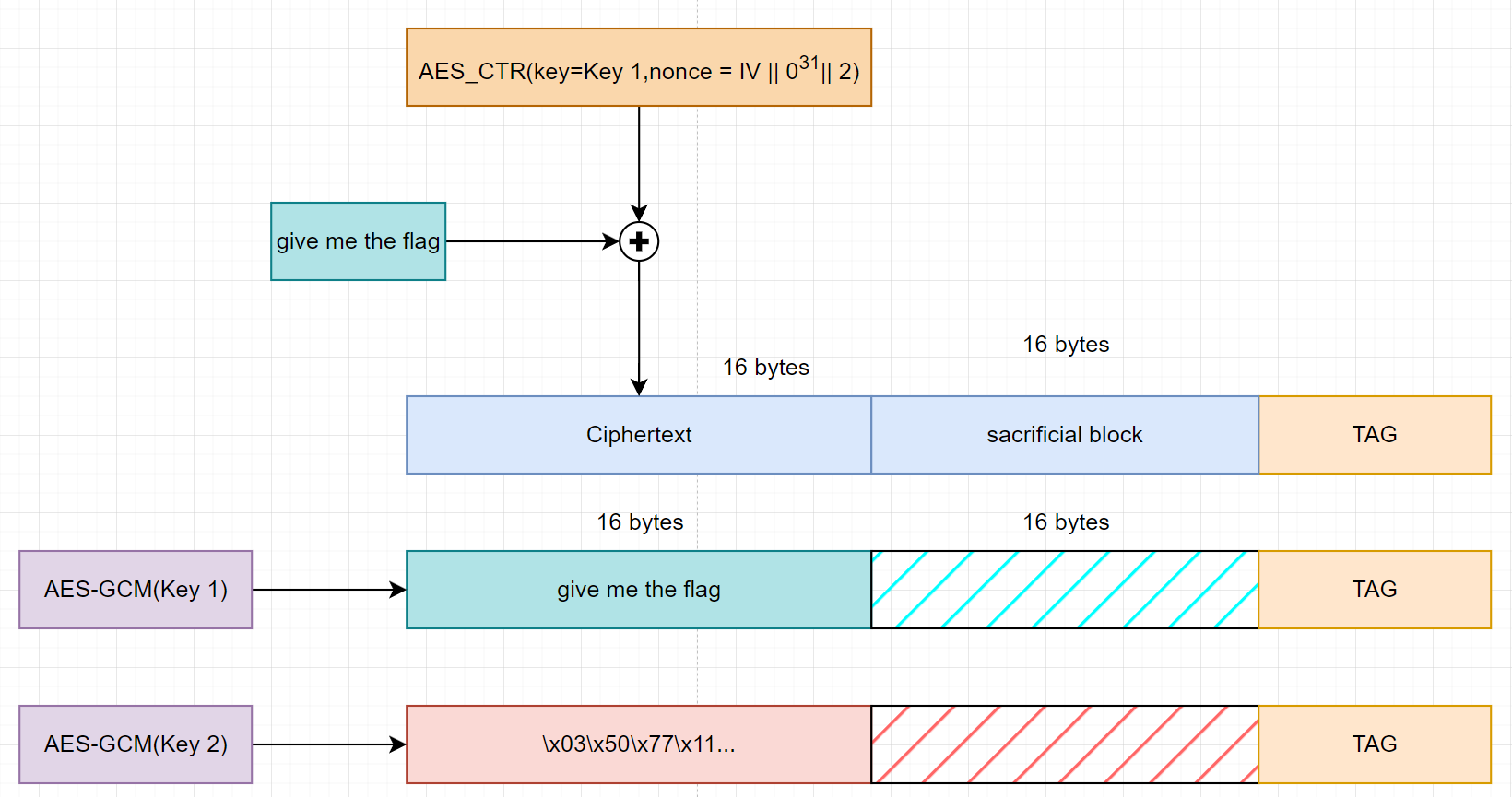For the case we just need one key to work.
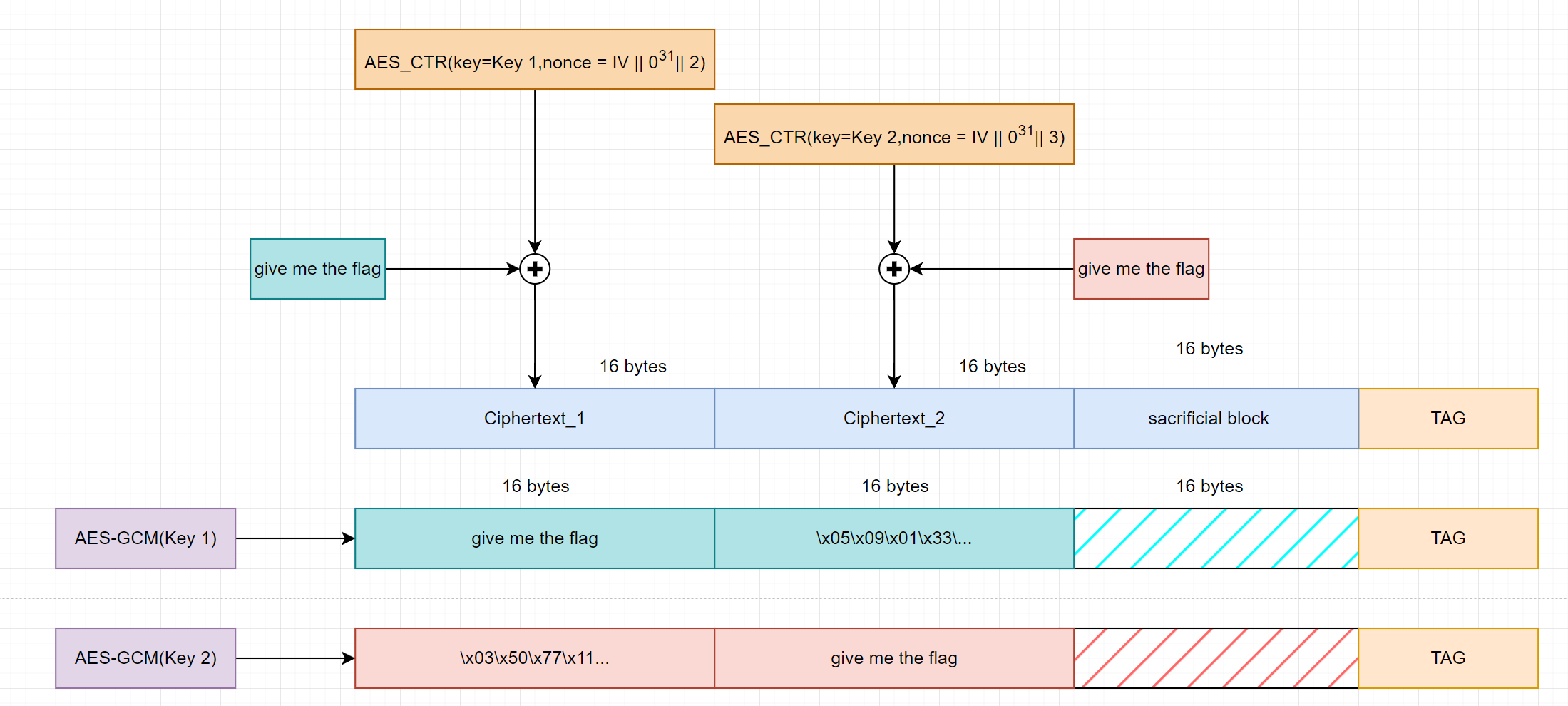Need plaintext for 2 keys
But in this case we will have a trash block at the front of the key 2 decryption. So to avoid this we have to brute some bytes of ciphertext 1 to make the decryption by key 2 have opening and ending comment for plaintext block 1.
Implementation:
We will be using SageMath to implement the POC because it support finite field arithmetic.
Convert data into field element and reverse:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
R.<x> = PolynomialRing(GF(2), 'x')
GHASH_modulus = x^128 + x^7 + x^2 + x + 1
K = GF(2^128, name='a', modulus=GHASH_modulus) # Define GF(2^128)
def bytes_to_bit_array(data):
bit_array = []
for byte in data:
bits = bin(byte)[2:].zfill(8)
bit_array.extend(map(int, bits))
return bit_array
def bytes_to_field_element(byte_array):
bin_arr = bytes_to_bit_array(byte_array)
return K(bin_arr)
def field_element_to_bytes(field_element):
bit_array = field_element.list()
byte_data = bytearray()
for i in range(0, len(bit_array), 8):
bits = bit_array[i:i+8]
byte_str = ''.join(str(bit) for bit in bits)
byte = int(byte_str, 2)
byte_data.append(byte)
return bytes(byte_data)
Calculation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
def attack_gcm_for_manyblock(message,aad=None):
'''
Attack for any message len, but aad must be a multiple of 16
input: message, aad
output: key1, key2, and poison ciphertext.
The function is proved is correct by using pycryptodome library. from from Crypto.Cipher import AES -> cipher = AES.new(key,AES.MODE_GCM)
'''
key1 = os.urandom(32)
key2 = os.urandom(32)
numberofblock = 0
message = pad(message,16)
numberofblock = numberofblock + len(message)//16
iv = os.urandom(12)
iv = bytes(iv)
'''
Because when calculating GHASH the input will have the form:
all of the element must be pad right to multiple of 16 bytes
aad || ciphertext after xoring with key stream from AES-CTR || len(aad) || len(ct)
'''
array_ct_fixed = []
if aad:
for i in range(0,len(aad),16):
array_ct_fixed.append(aad[i:i+16])
else :
array_ct_fixed = []
for i in range(2, numberofblock+2):
ct = encrypt_EBC_nonce(key1,message[(i-2)*16:(i-1)*16],iv+b'\x00'*3+bytes([i]))
array_ct_fixed.append(ct)
H1 = encrypt_ECB(key1,b'\x00'*16)
H2 = encrypt_ECB(key2,b'\x00'*16)
# nonce for T1 and T2 = iv||0^31||1
T1 = encrypt_EBC_nonce(key1,b'\x00'*16,iv+b'\x00'*3+b'\x01')
T2 = encrypt_EBC_nonce(key2,b'\x00'*16,iv+b'\x00'*3+b'\x01')
'''
def length_block(aad,msg): return len(aad) || len(msg) pad to 128 bit (16 bytes).
'''
LENBLOCK = length_block(0,len(message)+16) # +1 sacrificial block
if aad:
LENBLOCK = length_block(len(aad),len(message)+16)
LENBLOCK =bytes_to_field_element(LENBLOCK)
H1 = bytes_to_field_element(H1)
H2 = bytes_to_field_element(H2)
T1 = bytes_to_field_element(T1)
T2 = bytes_to_field_element(T2)
array_ct = [bytes_to_field_element(i) for i in array_ct_fixed]
LHS = H1^2 + H2^2
RHS_H1 = sum([H1^(len(array_ct)-(i)+2)*array_ct[i] for i in range(len(array_ct))])
RHS_H2 = sum([H2^(len(array_ct)-(i)+2)*array_ct[i] for i in range(len(array_ct))])
RHS = (RHS_H1 + RHS_H2) + (H1+H2)*LENBLOCK + T1 + T2
ct_need = LHS^-1*RHS
# add one block so recalculate tag:
tag_attack = RHS_H1 + ct_need*H1^2 + H1*LENBLOCK + T1
# ciphertext_attack = iv+fix_ct+ct_2+ tag_attack
ciphertext_attack = iv
if aad:
array_ct = array_ct[len(aad)//16:]
for i in range(0,len(array_ct)):
ciphertext_attack += field_element_to_bytes(array_ct[i])
ciphertext_attack += field_element_to_bytes(ct_need)
ciphertext_attack += field_element_to_bytes(tag_attack)
return key1,key2,ciphertext_attack
Constructing Salamander on AES GCM SIV:
About this mode of AES, see here. In the blog, I have depicted the different between the two functions GHASH and POLYVAL. GHASH is calculated using the ciphertext, but POLYVAL is calculated using the plaintext.
In AES-GCM-SIV, the output from POLYVAL function will be served as input to a AES-ECB encryption, which in turn (xor with nonce) is the input to AES-CTR encryption from plaintext to the ciphertext. So the approach making two authenticator function equal is not enough in this scenario.
Summary, AES-GCM-SIV will have this elements:
- $ \text{msg_auth_key,msg_enc_key = Key derivation(master key). we will denote}$ $H = \;\text{msg_auth_key} \; \cdot x^{-128} \; \text{and msg_enc_key} = K_e$
- $POVYVAL(H,P) = \sum_{i=0}^{n}(P_i \cdot H^{n+1-i}) = S_s$
- $\text{tag = AES-ECB(key=}K_E,POLYVAL(H,P))$
- $\text{C = AES-CTR(key}K_E,IV=tag)$
The plaintext block $P$ is consists of aad, plaintext, len(aad), len(plaintext).
So the approach for this will be fixed the tag first. And from that calculate \(S_{s,i} = \text{AES-EBC-Decrypt}(K_{E,i},tag)\)
Which will give us 2 linear equations will $2n$ variables. But out ciphertext need to be the same - by definition. So we have another constrain. \(C_{i,1} = C_{i,2}\).
Ciphertext is constructed using $AES-CTR$ and everything is on $GF(2)$ so the xor operation is just addition. Let $\text{key_stream1}$ and $\text{key_stream2}$ is the output of $AES-CTR$ using $K_{E,1}$ and $K_{E,2}$ respectively.
So we have to satisfy the equations:
\[\text{key_stream1}[i] + P_{i,1} = \text{key_stream2}[i] + P_{i,2}\]With give us $n$ more equations. So if our plaintext needed has $n$ blocks of 16 bytes and by adding $2$ sacrificial blocks to a total of $n+2$ blocks, we will have $2$ equations from $POLYVAL$, $n+2$ from $\text{key_stream}$ and $n$ from fixing our plaintext needed to a total of $2+n+2+n = 2\cdot(n+2)$ linear equations for $2\cdot(n+2)$ variables so it is sufficient to solve easily. All the equation can be written in matrix form.
\[P(\text{n blocks + 2 sacrificial block}) \; \Rightarrow \text{Matrix (n+2)x(n+2)}\] \[\begin{pmatrix} H_1^{n+3} & H_1^{n+2} & ... & H_1^{2} & 0 & 0 & ... & 0 \\ 0 & 0 & ... & 0 &H_2^{n+3} & H_2^{n+2} & ... & H_2^{2} \\ 1 & 0 & ... & 0 & 1 & 0 & .. & 0 \\ 0 & 1 & ... & 0 & 0 & 1 & .. & 0 \\ .\\ .\\ 0 & 0 & .. & 1 & 0 & 0 & .. & 1\\ 1 & 0 & ..& 0 & 0 & 0 & .. & 0 \\ 0 & 1 & .. & 0 & 0 & 0 & .. & 0 \\ . \\ . \\ 0 & 0 & .. & 1 & 0 & 0 & .. & 0 \end{pmatrix} \cdot X = \begin{pmatrix} S_{s1} + H_1^{n+3+len(aad)}\cdot aad_0 + H_1^{n+3+len(aad)-1} \cdot aad_1 + ... + H_1^{n+3+1} \cdot aad_{len(aad)-1}\\ S_{s2} + H_2^{n+3+len(aad)}\cdot aad_0 + H_2^{n+3+len(aad)-1} \cdot aad_1 + ... + H_2^{n+3+1} \cdot aad_{len(aad)-1}\\ \text{key_stream1}[0] + \text{key_stream2}[0]\\ \text{key_stream1}[1] + \text{key_stream2}[1]\\ .\\ .\\ \text{key_stream1}[n+2] + \text{key_stream2}[n+2]\\ \text{need_plaintext1}[0]\\ \text{need_plaintext1}[1]\\ .\\ .\\ \text{need_plaintext1}[n+2]\\ \end{pmatrix}\]Variants:
From the two matrix above, we can see that the variant from AES GCM still work here.
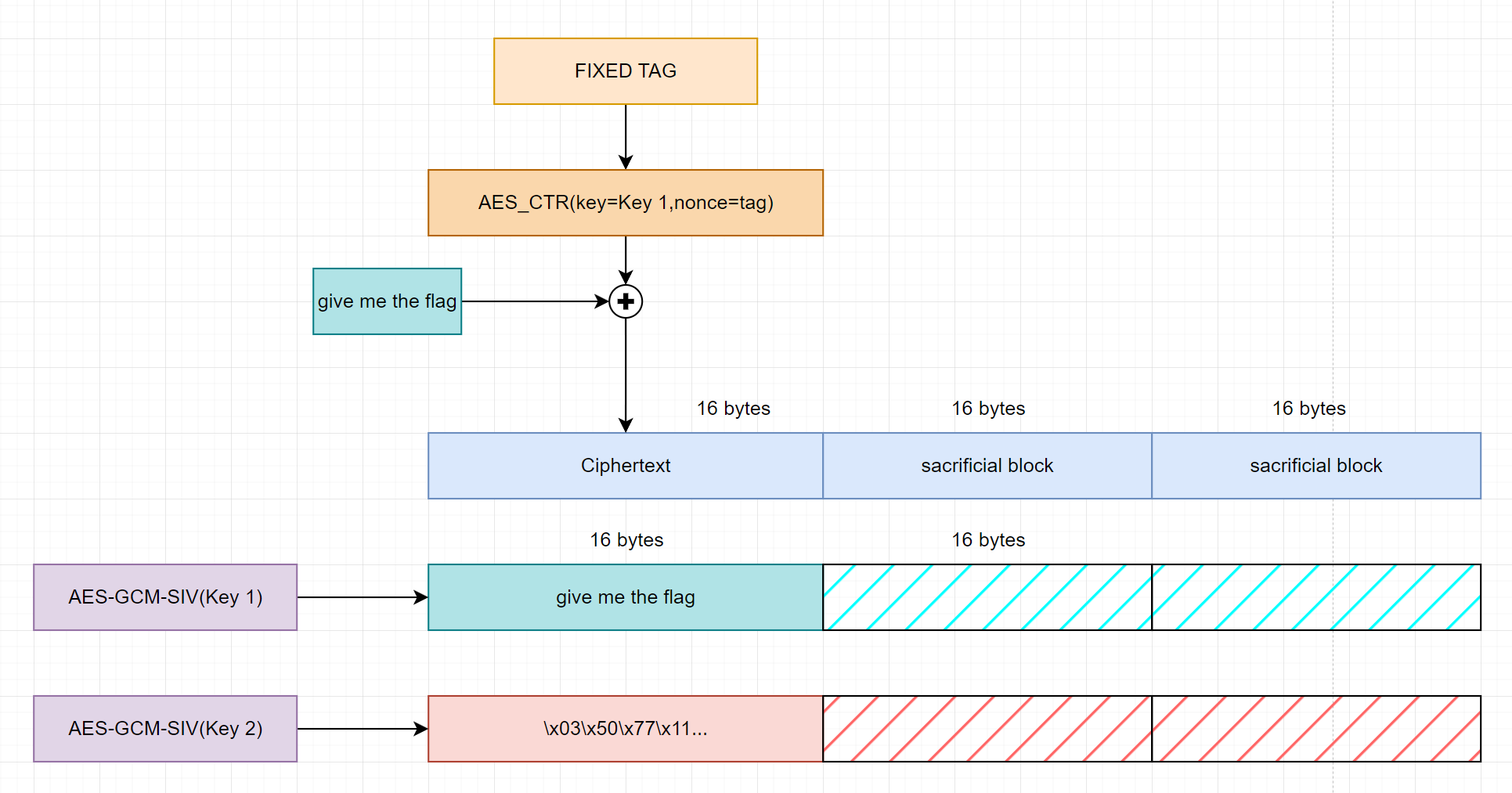For the case we just need one key to work.
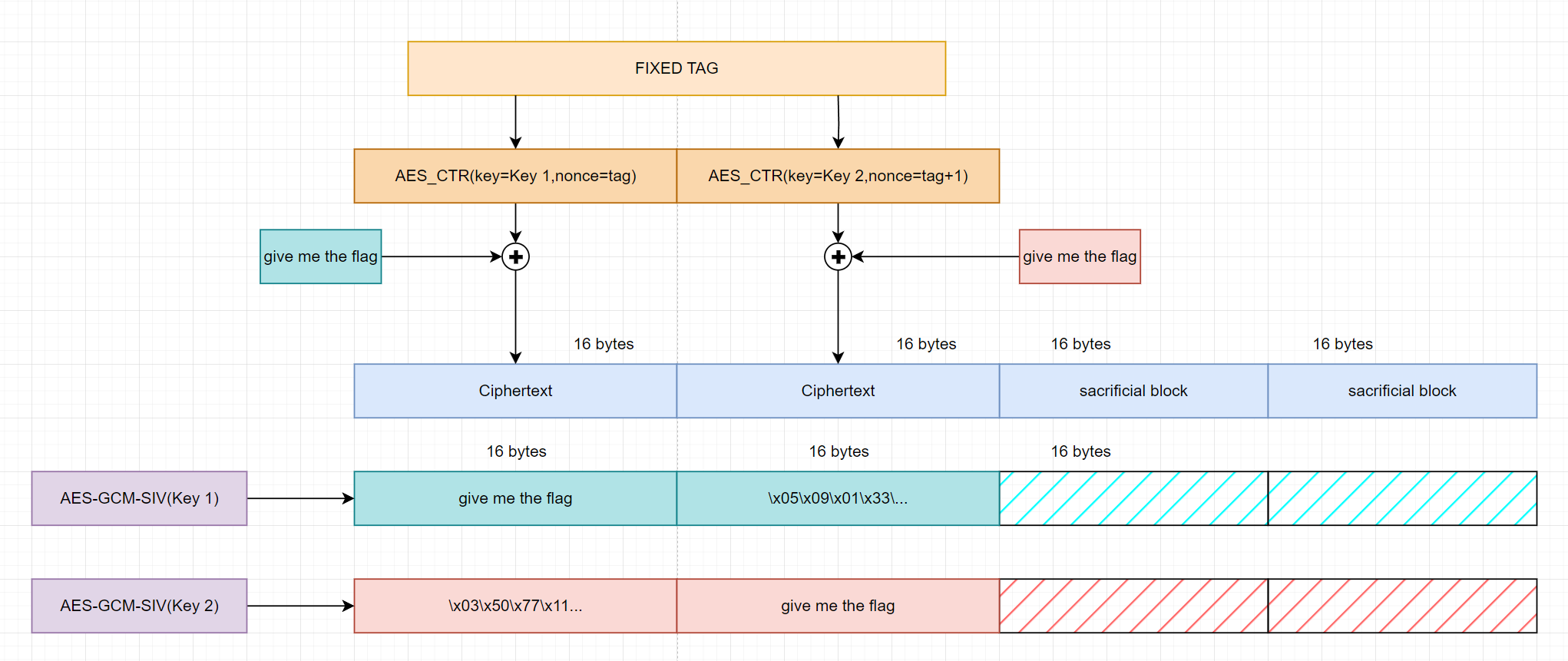Need plaintext for 2 keys
Implementation:
Convert data into field element and reverse:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
R.<x> = PolynomialRing(GF(2), 'x')
POLYVAL_modulus = x^128 + x^127 + x^126 + x^121 +1
K = GF(2**128, name='a', modulus=POLYVAL_modulus)
def bytes_to_bit_array(data):
bit_array = []
for byte in data:
bits = bin(byte)[2:].zfill(8)
bits = bits[::-1] # little endian - different between POLYVAL and GHASH
bit_array.extend(map(int, bits))
return bit_array
def bytes_to_field_element(byte_array):
bin_arr = bytes_to_bit_array(byte_array)
return K(bin_arr)
def field_element_to_bytes(field_element):
bit_array = field_element.list()
byte_data = bytearray()
for i in range(0, len(bit_array), 8):
bits = bit_array[i:i+8]
bits.reverse()
byte_str = ''.join(str(bit) for bit in bits)
byte = int(byte_str, 2)
byte_data.append(byte)
return bytes(byte_data)
def uint64_le(i):
return struct.pack(b'<Q', i)
def length_block(aad_length, ciphertext_length):
aad_length_bits = aad_length * 8
ciphertext_length_bits = ciphertext_length * 8
# Pack the lengths into a byte array using big-endian format
return uint64_le(aad_length_bits) + uint64_le(ciphertext_length_bits)
Check randomize a correct tag:
1
2
3
4
5
6
7
8
9
def check_polyval(msg_enc_key,nonce,tag):
cipher = AES.new(msg_enc_key, AES.MODE_ECB)
s = cipher.decrypt(tag)
check = False
if s[15] & 0x80 == 0:
check = True
nonce = nonce + b'\x00'*4
s = xor(s,nonce)
return check,s
Calculation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
def attack_many_block_gcm_siv(master_key1,master_key2,nonce,aad,need_plaintext):
'''
input: master_key1, master_key2 - 16 bytes, nonce - 12 bytes, aad multiple of 16 bytes, need_plaintext any length.
output: poison ciphertext + tag
The function is proved is correct by using a python github repos
'''
if aad == None:
aad = b''
if len(need_plaintext) % 16 != 0:
need_plaintext += b'\x00'*(16 - len(need_plaintext)%16)
num_blocks = len(need_plaintext)//16 + 2 # 2 sacrificial block
msg_auth_key1, msg_enc_key1 = GenerateKeys(master_key1,nonce) #Key derivation
msg_auth_key2, msg_enc_key2 = GenerateKeys(master_key2,nonce)
ciphertext = []
# brute tag
check_polyval1 = False
check_polyval2 = False
while not (check_polyval1 and check_polyval2):
tag = urandom(16)
check_polyval1,s1 = check_polyval(msg_enc_key1,nonce,tag)
check_polyval2,s2 = check_polyval(msg_enc_key2,nonce,tag)
# calculate counter in specification
counter_for_tag = bytearray(tag)
counter_for_tag[15] |= 0x80
counter_for_tag = bytes(counter_for_tag)
key_stream1 = []
key_stream2 = []
for i in range(num_blocks):
key_stream1.append(encrypt_ECB(msg_enc_key1,counter_for_tag))
key_stream2.append(encrypt_ECB(msg_enc_key2,counter_for_tag))
counter_for_tag = int.from_bytes(counter_for_tag,byteorder='little') + 1
counter_for_tag = counter_for_tag.to_bytes(16,byteorder='little')
inv = b'\x01'+b'\x00'*13+b'\x04'+b'\x92' # x^-128
inv = bytes_to_field_element(inv)
w1 = bytes_to_field_element(msg_auth_key1)*inv
w2 = bytes_to_field_element(msg_auth_key2)*inv
# set up matrix
matrix_size = 2*num_blocks
matrix_setup = []
plaintext_POVYVAL_key1 = [0 for i in range(matrix_size)]
plaintext_POVYVAL_key2 = [0 for i in range(matrix_size)]
for i in range(0,num_blocks):
plaintext_POVYVAL_key1[i] = w1^(num_blocks+1-i)
plaintext_POVYVAL_key2[i+num_blocks] = w2^(num_blocks+1-i)
matrix_setup.append(plaintext_POVYVAL_key1)
matrix_setup.append(plaintext_POVYVAL_key2)
for i in range(num_blocks):
tt = [0 for i in range(matrix_size)]
tt[i] = 1
tt[i+num_blocks] = 1
matrix_setup.append(tt)
for i in range(len(need_plaintext)//16):
tt = [0 for i in range(matrix_size)]
tt[i] = 1
matrix_setup.append(tt)
matrix_setup = Matrix(K,matrix_setup)
# A * X = B
rhs = []
aad_array = []
for i in range(0,len(aad),16):
aad_array.append(aad[i:i+16])
aad_field = []
for i in aad_array:
aad_field.append(bytes_to_field_element(i))
aad_field[::-1]
counter_for_aad = num_blocks+1
aad_POLYVAL_key1 = 0
aad_POLYVAL_key2 = 0
for i in aad_field:
counter_for_aad += 1
aad_POLYVAL_key1 += w1^counter_for_aad*i
aad_POLYVAL_key2 += w2^counter_for_aad*i
POLYVAL_key1 = bytes_to_field_element(s1) + w1*bytes_to_field_element(length_block(len(aad),16*num_blocks)) + aad_POLYVAL_key1
POLYVAL_key2 = bytes_to_field_element(s2) + w2*bytes_to_field_element(length_block(len(aad),16*num_blocks)) + aad_POLYVAL_key2
rhs.append(POLYVAL_key1)
rhs.append(POLYVAL_key2)
for i in range(num_blocks):
rhs.append(bytes_to_field_element(key_stream1[i]) + bytes_to_field_element(key_stream2[i]))
for i in range(len(need_plaintext)//16):
rhs.append(bytes_to_field_element(need_plaintext[i*16:(i+1)*16]))
rhs = vector(K,rhs)
result = matrix_setup.solve_right(rhs)
plaintext_1 =[]
for i in range(num_blocks):
plaintext_1.append(result[i])
for i in range(num_blocks):
ciphertext.append(bytes_to_field_element(key_stream1[i]) + plaintext_1[i])
for i in range(0,len(ciphertext)):
ciphertext[i] = field_element_to_bytes(ciphertext[i])
ciphertext = b''.join(ciphertext)
return ciphertext + tag
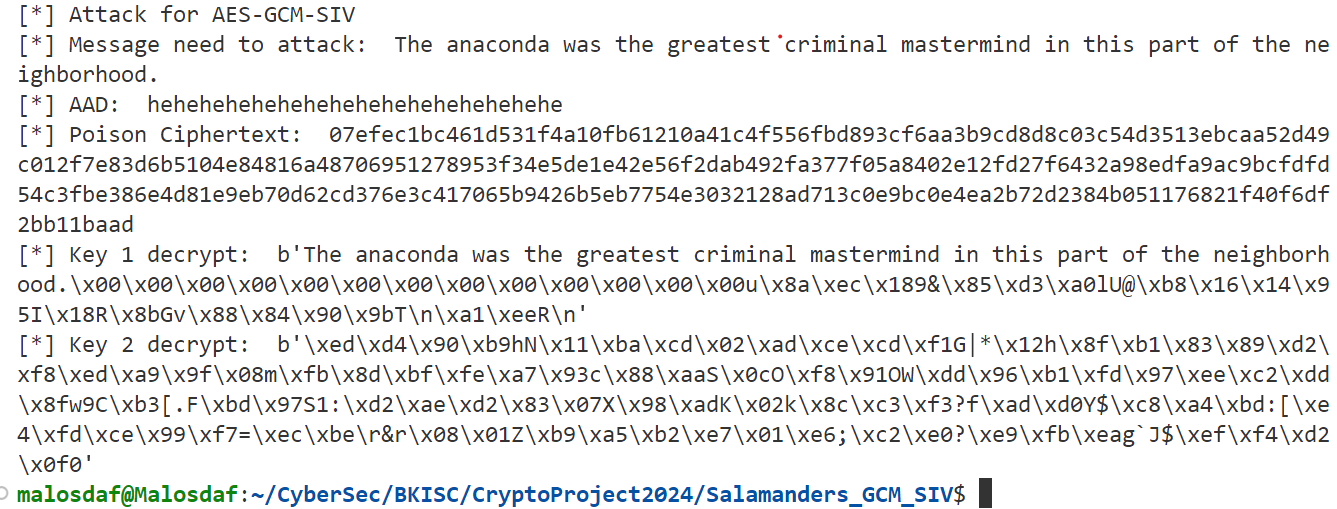Need plaintext for 2 keys
References
- Invisible Salamanders in AES-GCM-SIV
- Analysis of vulnerabilities in AES-GCM-SIV.
- Another Look at Security of GCM
- Examination of GCM security and associated issues.